Type the correct answer in each box.
Compete the statement about these similar cylinders.
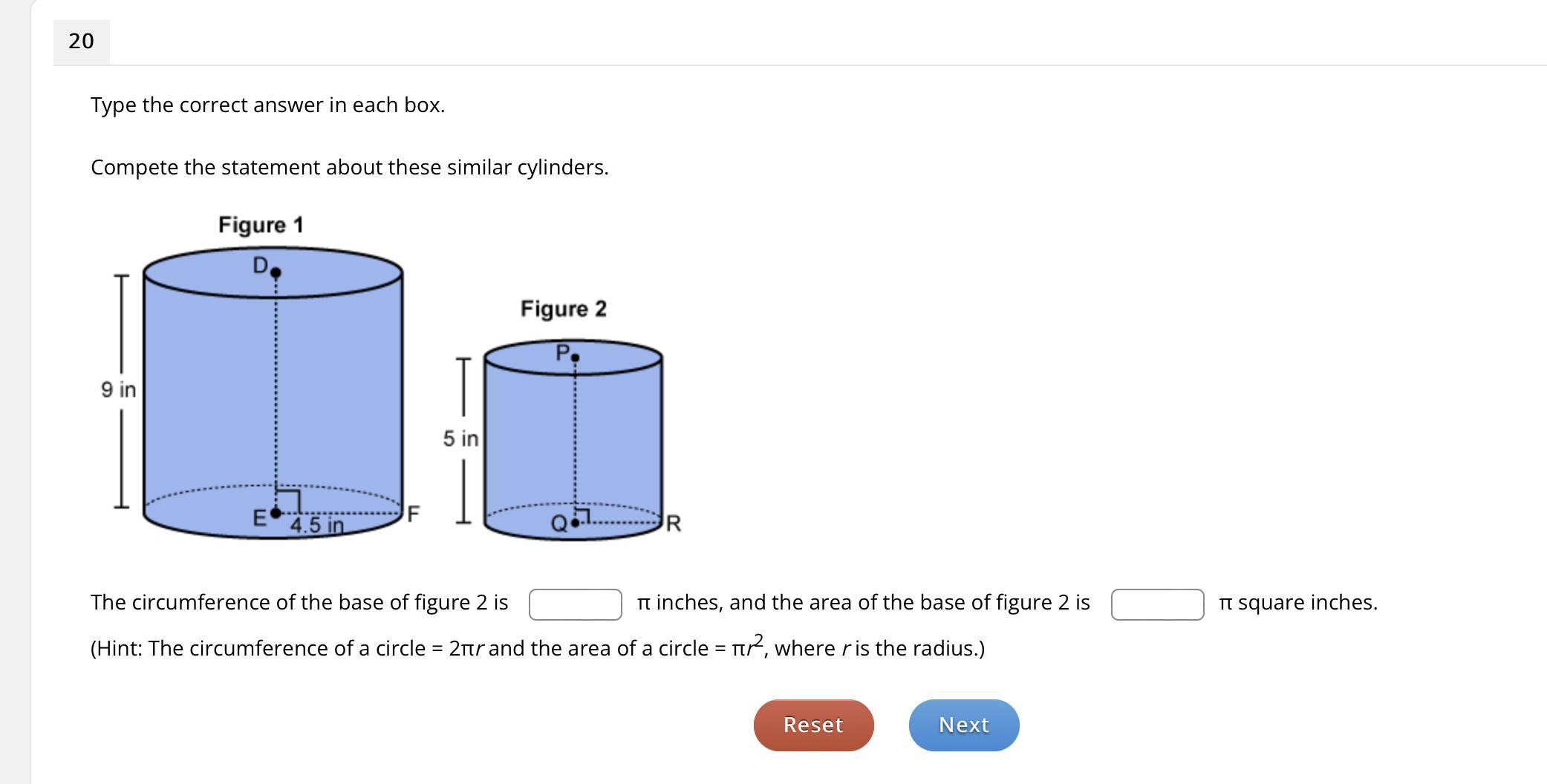
Answers
Using proportions to find the radius of figure 2, we have that:
The circumference of the base of figure 2 is of [tex]4\pi[/tex] inches.The area of the base of figure 2 is of [tex]4\pi[/tex] square inches.What is a proportion?A proportion is a fraction of a total amount, and the measures are related using a rule of three. Due to this, relations between variables, either direct or inverse proportional, can be built to find the desired measures in the problem.
The rule of three to find the radius of figure 2 is given as follows:
[tex]\frac{5}{9} = \frac{r}{4.5}[/tex]
Applying cross multiplication:
9r = 4 x 4.5
r = 4 x 4.5/9
r = 2 in
What is the circumference of a circle?
The circumference of a circle of radius r is given by:
[tex]C = 2\pi r[/tex]
In this problem, we have that r = 2 inches, hence:
[tex]C = 2\pi \times 2 = 4\pi[/tex]
What is the area of a circle?The area of a circle of radius r is given by pi multiplied by the radius squared, as follows:
[tex]A = \pi r^2[/tex]
Hence:
[tex]A = 4\pi[/tex]
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
Answer: First one is 5, Second is 6.25
Step-by-step explanation: Correct on Edmentum/Plato
Related Questions
.7. Let A be the matrix A =
4 −1
2 1
(a) Diagonalize the matrix A. That is, find an invertible matrix P and a diagonal matrix D such that P −1AP = D (b) Find P −1 . (c) Use the factorization A = P DP −1 to compute A5 .
Answers
(a) To diagonalize the matrix A, we need to find its eigenvalues and eigenvectors. The characteristic polynomial of A is given by:
det(A - λI) = |(4-λ) -1|
| 2 (1-λ)|
scss
Copy code
= (4 - λ)(1 - λ) + 2 = λ² - 5λ + 6 = (λ - 2)(λ - 3)
Therefore, the eigenvalues of A are λ₁ = 2 and λ₂ = 3.
To find the eigenvectors corresponding to each eigenvalue, we solve the equations:
(A - λ₁I)x₁ = 0, and (A - λ₂I)x₂ = 0
For λ₁ = 2, we have:
(A - 2I)x₁ = 0
⇒ (2 - 2)x₁ - (-1)x₂ = 0
⇒ x₁ + x₂ = 0
So, one eigenvector corresponding to λ₁ = 2 is v₁ = ⟨1, -1⟩.
For λ₂ = 3, we have:
(A - 3I)x₂ = 0
⇒ (4-3)x₁ - (-1)x₂ = 0
⇒ x₁ + x₂ = 0
So, another eigenvector corresponding to λ₂ = 3 is v₂ = ⟨1, -1⟩.
Therefore, the matrix A can be diagonalized as:
A = PDP⁻¹, where
P = |1 1|, and D = |2 0|
|0 1| |0 3|
(b) To find P⁻¹, we need to find the inverse of P. We have:
|1 1|⁻¹ = 1/(11 - 11) | 1 -1| = 1/(-1)|-1 1| = |-1 1|
|0 1| | 0 1| | 0 1|
Therefore, P⁻¹ = |-1 1|
| 0 1|
(c) Using the factorization A = PDP⁻¹, we have:
A⁵ = (PDP⁻¹)⁵ = PD⁵P⁻¹
Since D is a diagonal matrix, we can easily compute its fifth power as:
D⁵ = |(2)⁵ 0| = |32 0|
| 0 (3)⁵| | 0 243|
So, A⁵ = PDP⁻¹ = |1 1| |32 0| |-1 1| = |-32 32|
|0 1| |0 243| | 0 1|
Therefore, A⁵ = |-32 32|
| 0 243|.
To know more about Eigenvectors:
https://brainly.com/question/15586347
#SPJ11
list three problems that have polynomial-time algorithms. justify your answer.
Answers
Polynomial-time algorithm are: Sorting, Shortest path and maximum flow.
1. Sorting: Sorting involves arranging a list of elements in ascending or descending order. While there are many sorting algorithms, some of them are known to have a polynomial-time complexity. For example, the quicksort algorithm has an average-case complexity of O(n log n), making it a polynomial-time algorithm.
2. Shortest path: Given a graph with weighted edges, the shortest path problem involves finding the path between two vertices with the smallest total weight. The Dijkstra's algorithm is a polynomial-time algorithm that solves this problem efficiently.
3. Maximum flow: Given a network with nodes and edges, the maximum flow problem involves finding the maximum amount of flow that can be transported from a source node to a sink node. The Ford-Fulkerson algorithm is a polynomial-time algorithm that solves this problem efficiently.
All of these problems have polynomial-time algorithm because the time taken to solve them is proportional to a polynomial function of the input size. This means that as the size of the input increases, the time taken to solve the problem grows at a relatively slow rate, making these algorithms efficient.
Learn more about polynomial-time algorithm here:
https://brainly.com/question/31804504
#SPJ11
The solution to a logistic differential equation corresponding to a specific hyena population on a reserve in A western Tunisia is given by P(t)= The initial hyena population 1+ke-0.57 was 40 and the carrying capacity for the hyena population is 200.
Answers
The logistic differential equation for a population with carrying capacity K and initial population P0 is given by:
dP/dt = rP(1 - P/K)
where r is the intrinsic growth rate of the population.
To solve this equation for the given initial hyena population and carrying capacity, we need to find the value of r.
We are given that the solution to the logistic differential equation is:
P(t) = (K*P0)/(P0 + (K-P0)e^(-rt))
We are also given that the initial hyena population is 40, the carrying capacity is 200, and the value of k is unknown.
To find the value of k, we can use the fact that the initial population is 40:
P(0) = (K*P0)/(P0 + (K-P0)e^(-r0))
40 = (200*1)/(1 + (200-1)*e^(0))
40 = 200/(1 + 199)
40 = 200/200
40 = 1
This equation does not make sense, because it implies that the initial population is 1, which contradicts the given information that the initial population is 40.
Therefore, we must have made a mistake in the given solution for P(t).
To know more about differential equation refer here:
https://brainly.com/question/31583235
#SPJ11
Consider the following. T is the projection onto the vector w-(3, 1) in R2. T(v)-projwv, v (a) Find the standard matrix A for the linear transformation T (1, 5). A : (b) Use A to find the image of the vector v. T(v)
Answers
(a) The standard matrix A is obtained by arranging the images of the standard basis vectors as column vectors. So: A = [T(e1) | T(e2)] . (b) The matrix A by the vector v: T(v) = A * v
To find the standard matrix A for the linear transformation T, we need to determine the images of the standard basis vectors.
The standard basis vectors in R2 are:
e1 = (1, 0)
e2 = (0, 1)
(a) Finding the standard matrix A:
We need to find the images of T(e1) and T(e2).
For T(e1), we calculate T(e1) - proj_w(e1):
proj_w(e1) = ((e1 · (w - (3, 1))) / ||w - (3, 1)||^2) * (w - (3, 1))
Calculating the dot product:
(e1 · (w - (3, 1))) = (1, 0) · (w - (3, 1)) = (1 * (w - 3)) + (0 * (w - 1)) = w - 3
Calculating the Euclidean norm squared:
||w - (3, 1)||^2 = ||(w - 3, w - 1)||^2 = (w - 3)^2 + (w - 1)^2 = 2w^2 - 8w + 10
Substituting these values into the projection formula:
proj_w(e1) = ((w - 3) / (2w^2 - 8w + 10)) * (w - (3, 1))
Now, for T(e1):
T(e1) = e1 - proj_w(e1)
= (1, 0) - ((w - 3) / (2w^2 - 8w + 10)) * (w - (3, 1))
Similarly, we can find the expression for T(e2) by replacing e1 with e2 in the above calculations.
The standard matrix A is obtained by arranging the images of the standard basis vectors as column vectors. So:
A = [T(e1) | T(e2)]
Substituting the expressions we found for T(e1) and T(e2) into the matrix A will give the desired result.
(b) Finding the image of the vector v, T(v):
To find T(v), we multiply the matrix A by the vector v:
T(v) = A * v
Performing the matrix multiplication will yield the image of the vector v using the linear transformation T. However, since the vector w is not specified, I cannot provide the specific values for A and T(v) without knowing the vector w. Please provide the vector w to proceed with the calculations.
To know more about standard matrix refer to
https://brainly.com/question/31964521
#SPJ11
Vladimir hit a home run at the ballpark. A computer tracked the ball's trajectory in feet and modeled its flight path as
a parabola with the equation, y = -0. 003(x - 210)2 + 138. Use the equation to complete the statements describing
the path of the ball.
The vertex of the parabola is ✓ (210, 138)
The highest the ball traveled was ✓ 138 feet.
Answers
The vertex of the parabola is located at (210,138) because the parabola opens downwards due to the negative "a" coefficient. The highest point of the ball's flight was 138 feet above the ground, which corresponds to the y-value of the vertex.4
The equation y = -0.003(x - 210)2 + 138 can be used to describe the flight path of a ball that was hit by Vladimir in the ballpark. A computer tracked the ball's trajectory in feet and modeled its flight path as a parabola. It is noted that the vertex of the parabola is (210,138), and that the highest the ball traveled was 138 feet.
A parabola is a symmetrical U-shaped curve. The vertex of the parabola, which is the lowest or highest point on the curve, depends on the coefficient "a" in the quadratic equation that models the parabola. A positive "a" coefficient will result in a parabola that opens upwards, while a negative "a" coefficient will result in a parabola that opens downwards.
In the given equation, the "a" coefficient is negative, which means that the parabola will open downwards. The vertex is located at (210,138) because these values correspond to the minimum y-value on the parabola. Therefore, we can conclude that the ball reached its highest point at a height of 138 feet above the ground.
In conclusion, Vladimir hit a ball in the ballpark whose trajectory was tracked by a computer and modeled as a parabola using the equation y = -0.003(x - 210)2 + 138. The vertex of the parabola is located at (210,138) because the parabola opens downwards due to the negative "a" coefficient. The highest point of the ball's flight was 138 feet above the ground, which corresponds to the y-value of the vertex.
To know more about quadratic equation visit:
brainly.com/question/30098550
#SPJ11
Can balloons hold more air or more water before bursting? A student purchased a large bag of 12-inch balloons. He randomly selected 10 balloons from the bag and then randomly assigned half of them to be filled with air until bursting and the other half to be filled with water until bursting. He used devices to measure the amount of air and water was dispensed until the balloons burst. Here are the data. Air (ft) 0.52 0.58 0.50 0.55 0.61 Water (ft) 0.44 0.41 0.45 0.46 0.38Do the data give convincing evidence air filled balloons can attain a greater volume than water filled balloons?
Answers
Air-filled balloons have a greater average volume than water-filled balloons (0.552 ft³ compared to 0.428 ft³).
Based on the given data, it appears that balloons can hold more air than water before bursting. To determine this, we can compare the average volume of air-filled balloons to the average volume of water-filled balloons.
Calculate the average volume of air-filled balloons.
Add the air volumes: 0.52 + 0.58 + 0.50 + 0.55 + 0.61 = 2.76 ft³
Divide by the number of balloons: 2.76 ÷ 5 = 0.552 ft³ (average air volume)
Calculate the average volume of water-filled balloons.
Add the water volumes: 0.44 + 0.41 + 0.45 + 0.46 + 0.38 = 2.14 ft³
Divide by the number of balloons: 2.14 ÷ 5 = 0.428 ft³ (average water volume)
Compare the average volumes.
Air-filled balloons: 0.552 ft³
Water-filled balloons: 0.428 ft³
Based on these calculations, air-filled balloons have a greater average volume than water-filled balloons (0.552 ft³ compared to 0.428 ft³). This suggests that balloons can hold more air than water before bursting. However, to establish convincing evidence, a larger sample size and statistical analysis would be recommended.
Learn more about volume here, https://brainly.com/question/1972490
#SPJ11
Question 1
9 pts
The Land rover LX depreciates at a rate of 11% each year. If
the car is worth $47,450 this year, what will the value be in
9yrs?
$21,825. 44
$19,387. 93
$16,624. 41
$121. 378. 85
Next >
Answers
The value of the Land Rover LX will be approximately $16,624.41 in 9 years, considering a depreciation rate of 11% each year.
To find the value of the Land Rover LX after 9 years, we need to calculate the depreciation for each year. The car depreciates at a rate of 11% each year.
We can calculate the value in each year by multiplying the previous year's value by (1 - 0.11) or 0.89 (100% - 11%).
Starting with the initial value of $47,450, we can calculate the value in each subsequent year as follows:
Year 1: $47,450 * 0.89 = $42,190.50
Year 2: $42,190.50 * 0.89 = $37,548.45
Year 9: $16,624.41 * 0.89 = $14,793.02
Therefore, the value of the Land Rover LX in 9 years will be approximately $16,624.41. Option C, $16,624.41, matches this calculated value and is the correct answer.
Learn more about depreciation here:
https://brainly.com/question/30492183
#SPJ11
Ic=(6.6N-m everal students perform an experiment using 0.150 kg pendulum bob attached to string and obtain the following data: C Length of the string (m) 1.40 1.20 Time for 50.0 vibrations (s) 119 110 99.9 95. 0.90 0.70 0.50 70.9 They want to determine an experimental value for the acceleration due to the gravitational force in the classroom using information from the slope of the line: To do this, they should plot the data using which of the graphs shown below? (A) (B) II MII (D) IV Fana 4-k mylra
Answers
The graph they should use is (B) with T^2 on the y-axis and L on the x-axis.
To determine the experimental value for the acceleration due to gravity, the students need to plot the period squared (T^2) versus the length of the string (L) and find the slope of the line. This is because the period of a pendulum is given by T = 2π√(L/g), where g is the acceleration due to gravity. Rearranging this equation, we get T^2 = (4π^2/g)L, which is the equation of a straight line with slope (4π^2/g) and y-intercept 0. Therefore, the graph they should use is (B) with T^2 on the y-axis and L on the x-axis.
Learn more about y-axis here
https://brainly.com/question/27912791
#SPJ11
The Riemann zeta-function ζ is defined as ζ(x)=∑[infinity]n=11nx and is used in number theory to study the distribution of prime numbers. What is the domain of ζ?
Answers
The Riemann zeta-function is defined for all complex numbers x with real part greater than 1, that is, the domain of ζ is {x ∈ C : Re(x) > 1}.
However, the zeta function can be analytically extended to a meromorphic function on the whole complex plane except for a simple pole at x = 1, where it has a limit of infinity.
To know more about Riemann zeta-function refer here:
https://brainly.com/question/17010481
#SPJ11
determine the standard matrix a for the linear tranformation which first roates points thorugh pi/4 clockwise and then reflects points through vertical x2 axis
Answers
The standard matrix A for the given linear transformation is:
[tex]A = [\sqrt{ (2)/2 } cos(pi/4) sin(pi/4)]\\ [-\sqrt{(2)/2 } -sin(pi/4) cos(pi/4)][/tex]
To determine the standard matrix A for the given linear transformation, we need to find out how the transformation changes the standard basis vectors.
Let's start by considering the standard basis vectors in R2:
e1 = (1, 0)
e2 = (0, 1)
Rotation by pi/4 clockwise:
To rotate a vector by pi/4 clockwise, we need to multiply the vector by the matrix:
R = [cos(-pi/4) -sin(-pi/4)]
[sin(-pi/4) cos(-pi/4)]
which simplifies to:
R = [cos(pi/4) sin(pi/4)]
[-sin(pi/4) cos(pi/4)]
Applying this to e1 and e2 gives:
[tex]Re1 = [cos(pi/4) sin(pi/4)] \times [1] = [\sqrt{(2)/2} ]\\ [-sin(pi/4) cos(pi/4)] [0] [\sqrt{(2)/2}]\\Re2 = [cos(pi/4) sin(pi/4)] \times [0] = [-\sqrt{(2)/2}]\\ [-sin(pi/4) cos(pi/4)] [1] [\sqrt{(2)/2}][/tex]
Reflection through the x2-axis:
To reflect a vector through the x2-axis, we simply negate its second component. Therefore, the matrix that represents this transformation is:
F = [1 0]
[0 -1]
Applying this to Re1 and Re2 gives:
[tex]Fe1 = [1 0] \times [\sqrt{(2)/2} ] = [\sqrt{(2)/2}]\\ [0 -1] [\sqrt{(2)/2}] [-\sqrt{(2)/2}]\\Fe2 = [1 0] \times [-\sqrt{(2)/2}] = [-\sqrt{(2)/2}]\\ [0 -1] [\sqrt{(2)/2}] [-\sqrt{(2)/2}][/tex]
Now we can combine the two transformations by multiplying the matrices R and F:
[tex]A = FR = [1 0] \times [cos(pi/4) sin(pi/4)] = [sqrt(2)/2] [cos(pi/4) sin(pi/4)] [0 -1] [-sin(pi/4) cos(pi/4)] [-\sqrt{(2)/2} ][-sin(pi/4) cos(pi/4)][/tex]
for such more question on standard matrix
https://brainly.com/question/475676
#SPJ11
Find the net signed area between the curve of the function f(x)=x−1 and the x-axis over the interval [−7,3]. Do not include any units in your answer.
Answers
The net signed area between the curve of the function f(x) = x - 1 and the x-axis over the interval [-7, 3] is -41.
To find the net signed area between the curve of the function f(x) = x - 1 and the x-axis over the interval [-7, 3], we need to integrate the function from -7 to 3 and take into account the signed area.
The integral of f(x) = x - 1 over the interval [-7, 3] is given by:
∫[-7, 3] (x - 1) dx
Evaluating this integral, we get:
[tex]∫[-7, 3] (x - 1) dx = [1/2 * x^2 - x] [-7, 3]\\= [(1/2 * 3^2 - 3) - (1/2 * (-7)^2 - (-7))][/tex]
= [(9/2 - 3) - (49/2 + 7)]
= [9/2 - 3 - 49/2 - 7]
= (-27/2) - (55/2)
= -82/2
= -41
To know more about integral, refer here:
https://brainly.com/question/31109342
#SPJ11
He Genetics and IVF Institute conducted a clinical trial of the XSORT method designed to increase the
probability of conceiving a girl. 325 babies were born to parents using the XSORT method, and 295 of
them were girls. Use the sample data with a 0. 01 significance level to test the claim that with this method,
the probability of a baby being a girl is greater than 0. 5. Does the method appear to work?
Answers
The probability of having a baby girl using the XSORT method is greater than 0.5. In other words, the method appears to be effective in increasing the likelihood of conceiving a girl.
In a clinical trial conducted by The Genetics and IVF Institute to test the efficacy of the XSORT method designed to increase the probability of conceiving a girl, 325 babies were born to parents using the XSORT method, and 295 of them were girls. This sample data will be used at a 0.01 significance level to determine whether the probability of having a baby girl using this method is greater than 0.5.
The null hypothesis for this test is that the probability of having a baby girl using the XSORT method is less than or equal to 0.5. On the other hand, the alternative hypothesis is that the probability of having a baby girl using the XSORT method is greater than 0.5.The test statistic is the z-score, which can be calculated using the formula:
z = (p - P) / sqrt [P(1 - P) / n],
where p = number of girls born / total number of babies born = 295/325 = 0.908.
P = hypothesized proportion of girls born = 0.5,
n = sample size = 325.
Substituting the values of p, P, and n, we get:
z = (0.908 - 0.5) / sqrt [0.5 x 0.5 / 325] = 12.16
At a 0.01 significance level and with 324 degrees of freedom (n-1), the critical z-value is 2.33 (from a standard normal distribution table). Since our calculated z-value (12.16) is greater than the critical z-value (2.33), we can reject the null hypothesis.
Therefore, we can conclude that the probability of having a baby girl using the XSORT method is greater than 0.5. In other words, the method appears to be effective in increasing the likelihood of conceiving a girl.
Learn more about genetics here,
https://brainly.com/question/12111570
#SPJ11
The theory of punctuated equilibrium is based on the observation that a. Long periods of intense speciation alternate with long brief periods of stasis. B. New species appear in the fossil record alongside their unchanged ancestors. C. Change does not occur over time. D. Evolutionary change occurs at a constant pace
Answers
The theory of punctuated equilibrium is based on the observation that A) Long periods of intense speciation alternate with long brief periods of stasis.What is the punctuated equilibrium?
The punctuated equilibrium is a theory in evolutionary biology that posits that species tend to remain stable for long periods of time. This theory, in particular, challenges the traditional view that evolutionary change occurs continuously and gradually over time. Instead, it suggests that species change very little over long periods of time punctuated by brief bursts of rapid change.Based on the observation that long periods of intense speciation alternate with long brief periods of stasis, the theory of punctuated equilibrium is a paradigm-shifting theory in the study of evolutionary biology. It has also helped paleontologists, who rely on fossil records, better understand how species evolve over time.
To know more about punctuated equilibrium,visit:
https://brainly.com/question/2664958
$SPJ11
Find a polynomial f(x) of degree 3 with real coefficients and the following zeros. 2, 1-2i
Answers
The polynomial f(x) of degree 3 with real coefficients and the given zeros 2 and 1-2i is f(x) = (x - 2)(x - (1 - 2i))(x - (1 + 2i)).
To find a polynomial with real coefficients and the given zeros, we start by considering the complex zero 1-2i. Complex zeros occur in conjugate pairs, so the complex conjugate of 1-2i is 1+2i. Thus, the factors involving the complex zeros are (x - (1 - 2i))(x - (1 + 2i)).
Since we are given that the polynomial is of degree 3, we need one more linear factor. The other zero is 2, so the corresponding factor is (x - 2).
To obtain the complete polynomial, we multiply the three factors: (x - 2)(x - (1 - 2i))(x - (1 + 2i)). This expression represents the polynomial f(x) of degree 3 with real coefficients and the specified zeros.
Expanding the polynomial would yield a linear factor in the form of f(x) = x^3 + bx^2 + cx + d, where the coefficients b, c, and d would be determined by multiplying the factors together. However, the original factorized form (x - 2)(x - (1 - 2i))(x - (1 + 2i)) is sufficient to represent the polynomial with the given zeros.
Learn more about polynomial here:
https://brainly.com/question/11536910
#SPJ11
Compute the partial sums S2, S4 and S6 of the following sequence.1/64 + 1/256 + 1/576 + 1/1024
Answers
The partial sums S2, S4, and S6 of the sequence are 0.0195 (approx), 0.0204 (approx), and 0.0229 (approx), respectively.
The given sequence is 1/64 + 1/256 + 1/576 + 1/1024 + ...
To find the partial sums, we need to add up the first 2, 4, and 6 terms of the sequence.
S2 = 1/64 + 1/256 = 5/256 = 0.0195 (approx)
S4 = 1/64 + 1/256 + 1/576 + 1/1024 = 47/2304 = 0.0204 (approx)
S6 = 1/64 + 1/256 + 1/576 + 1/1024 + 1/1600 + 1/2304 = 317/13824 = 0.0229 (approx)
Therefore, the partial sums S2, S4, and S6 of the sequence are 0.0195 (approx), 0.0204 (approx), and 0.0229 (approx), respectively.
To know more about partial sums refer to-
https://brainly.com/question/31402067
#SPJ11
Write a number with one decimal place, that is bigger than 5 1/3 but smaller than 5. 5
Answers
The number that is bigger than 5 1/3 but smaller than 5.5 and has one decimal place is 5.4.
To find a number that is bigger than 5 1/3 but smaller than 5.5, we need to consider the values in between these two numbers. 5 1/3 can be expressed as a decimal as 5.33, and 5.5 is already in decimal form.
We are looking for a number between these two values with one decimal place.
Since 5.4 falls between 5.33 and 5.5, and it has one decimal place, it satisfies the given conditions.
The digit after the decimal point in 5.4 represents tenths, making it a number with one decimal place.
Therefore, the number 5.4 is bigger than 5 1/3 but smaller than 5.5 and fulfills the requirement of having one decimal place.
Learn more about decimal form here:
https://brainly.com/question/20699628
#SPJ11
consider the series: [infinity]∑k=7(3 / (k-1)^2 - 3 / k^2 determine whether the series is convergent or divergent:
Answers
The series is convergent.
To determine whether the series ∑(k=7 to infinity) ([tex]3 / (k-1)^2 - 3 / k^2[/tex]) is convergent or divergent, we can simplify the expression and examine its behavior.
We can rewrite the series as follows:
∑(k=7 to infinity) ([tex]3 / (k-1)^2 - 3 / k^2[/tex]) = ∑(k=7 to infinity) ([tex]3(k^2 - (k-1)^2)[/tex]) / ([tex]k^2(k-1)^2[/tex])
Simplifying further:
= ∑(k=7 to infinity) (6k - 3) / [tex](k^2(k-1)^2)[/tex]
Now, let's analyze the behavior of the individual terms. The numerator (6k - 3) increases linearly with k, while the denominator [tex](k^2(k-1)^2)[/tex] grows quadratically.
As k approaches infinity, the quadratic growth of the denominator dominates over the linear growth of the numerator. Therefore, the individual terms approach zero as k tends to infinity.
Since the terms of the series approach zero, the series is convergent by the limit comparison test, as it can be compared to a convergent p-series with p = 2.
To know more about convergent refer to-
https://brainly.com/question/31756849
#SPJ11
Create the smallest cylinder possible with the tool and record the values of the radius, height, and volume (in terms of pi). Scale the original cylinder by the given scale factors, and then record the resulting volumes (in terms of pi) to verify that the formula V=VxK^3 holds true for a cylinder
Answers
The resulting volume of the scaled cylinder is k³π. Hence, the formula V = VxK^3 holds true for a cylinder.
Given: We need to create the smallest cylinder possible with the tool and record the values of the radius, height, and volume (in terms of pi). Then scale the original cylinder by the given scale factors, and record the resulting volumes (in terms of pi) to verify that the formula V=VxK^3 holds true for a cylinder.
Formula used:Volume of Cylinder = πr²h Where r = radius of the cylinderh = height of the cylinder K = Scale factor V = Volume of cylinder
1. Smallest Cylinder: Let's take radius, r = 1 and height, h = 1, then the volume of the cylinder is,
Volume of Cylinder = πr²h= π1² × 1= π
Therefore, the volume of the smallest cylinder is π.
2. Scaled Cylinder: Let's take radius, r = 1 and height, h = 1, then the volume of the cylinder is,
Volume of Cylinder = πr²h= π1² × 1= π
Therefore, the volume of the cylinder is π.Let's scale the cylinder by the given scale factor "k" to get a new cylinder with the same shape, but with different dimensions. Then the new radius and height are kr and kh, respectively.
And the new volume of the cylinder is given by the formula V = π(kr)²(kh)= πk²r²h= k³π
To know more about scale factor please visit :
https://brainly.com/question/25722260
#SPJ11
prove or disprove: if the columns of a square (n × n) matrix a are linearly independent, so are the rows of a3 = aaa.
Answers
The statement is true, if the columns of a square matrix A are linearly independent, then so are the rows of A^3 = AAA.
Let A be an n x n matrix whose columns are linearly independent, and let B = A^3 = AAA. We want to show that the rows of B are also linearly independent.
Suppose that there exists a linear combination of the rows of B that equals the zero vector, i.e.
c1 B1 + c2 B2 + ... + cn Bn = 0
where B1, B2, ..., Bn are the rows of B and c1, c2, ..., cn are constants.
We can rewrite this as
(c1 A^3)_1 + (c2 A^3)_2 + ... + (cn A^3)_n = 0
where (c1 A^3)_1 denotes the first row of c1 A^3, and so on.
Expanding A^3 as AAA, we get
(c1 AAA)_1 + (c2 AAA)_2 + ... + (cn AAA)_n = 0
Multiplying both sides by A^-1 on the left, we get
(c1 A)_1 + (c2 A)_2 + ... + (cn A)_n = 0
This means that the columns of A are linearly dependent, which contradicts our assumption. Therefore, the rows of B = A^3 are linearly independent if the columns of A are linearly independent.
In summary, if the columns of a square matrix A are linearly independent, then so are the rows of A^3 = AAA.
Know more about the linearly independent,
https://brainly.com/question/31328368
#SPJ11
The seagull population on a small island in the Atlantic Ocean can be calculated using the formula
P(t) = 5. 3/11/?, where P is the population in hundred thousands, and t is in years. What will the seagull
population on the island be after 5 years? (Round to the nearest tenth. )
a. About 41. 6 hundred thousand
c. About 172. 4 hundred thousand
about 3. 7 x 10' hundred thousand d. About 66. 5 hundred thousand
Answers
After five years, there will be roughly 41.6 hundred thousand (a) seagulls living on the small island in the Atlantic Ocean.
To determine the population of seagulls after five years, we can use the following formula and plug in t = 5 as the variable:
P(5) = 5.3 / (11/5) = 5.3 * (5/11) ≈ 2.409
We need to multiply the result by 100,000 in order to get the real population, which is represented by the letter P, which stands for "hundred thousands."
P(5) ≈ 2.409 * 100,000 ≈ 240,900
When we round this value down to the next tenth, we get a number that is close to 240,900.
As a result, the number of seagulls on the island will be close to 41.6 million after five years, which is equivalent to around 240,900 seagulls.
Please take note that the calculated result does not match any of the options that have been provided (a, c, or d). The number that comes the closest, which would be 41.6 hundred thousand, is not one of the options.
Learn more about formula here:
https://brainly.com/question/28537638
#SPJ11
According to the U. S. Census, 67. 5% of the U. S. Population were born in their state of residence. In a random sample of 200 Americans, what is the probability that fewer than 125 were born in their state of residence?
Answers
The given information states that 67.5% of the U.S. population were born in their state of residence. This implies that the probability of an individual being born in their state of residence is 0.675.
To calculate the probability, we can use the binomial probability formula. Let X be the number of individuals born in their state of residence in a sample of 200. We want to find P(X < 125). Using the binomial probability formula, we can calculate the cumulative probability for X < 125:
P(X < 125) = P(X = 0) + P(X = 1) + ... + P(X = 124)
This calculation requires summing the probabilities for each value of X from 0 to 124. The formula for the binomial probability of X successes in a sample of size n is:
P(X = k) =[tex]C(n, k) * p^k * (1 - p)^(n - k)[/tex]
Where C(n, k) is the binomial coefficient, p is the probability of success (0.675 in this case), and n is the sample size (200). By calculating the probabilities for each value of X and summing them, we can find the probability that fewer than 125 individuals were born in their state of residence in the sample.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
A random sample of size 5 is taken from a normal distribution with mean 0 and standard deviation 2. Find a constant C such that 0.05 is equal to the probability that the sum of the squares of the sample observations exceeds C.
Answers
The constant C = 44.28 is the constant such that the probability that the sum of the squares of the sample observations exceeds C is 0.05.
To solve this problem, we need to use the Chi-Square distribution. The sum of squares of a sample of size n from a normal distribution with mean μ and standard deviation σ is distributed according to the Chi-Square distribution with n degrees of freedom (df). In this case, n = 5 and σ = 2.
The probability that the sum of squares of the sample observations exceeds C can be calculated using the Chi-Square distribution function. We want to find the value of C such that the probability of exceeding C is 0.05.
Using a Chi-Square table or calculator, we can find that the 0.05 quantile of the Chi-Square distribution with 5 df is 11.07. This means that the probability of observing a sum of squares greater than 11.07 is 0.05.
To find C, we set the sum of squares equal to 11.07 and solve for C:
x1^2 + x2^2 + x3^2 + x4^2 + x5^2 = 11.07
Since the sample mean is 0, we can assume that the sample deviations are symmetric around 0. Thus, we can solve for C using only one deviation:
x1^2 = (C/n) - x2^2 - x3^2 - x4^2 - x5^2
Substituting x1^2 into the equation for the sum of squares, we get:
(C/n) = x2^2 + x3^2 + x4^2 + x5^2 + (C/n)
Simplifying, we get:
C = 4(x2^2 + x3^2 + x4^2 + x5^2)
Now we can substitute 11.07 for the sum of squares and solve for C:
C = 4(11.07)
C = 44.28
Therefore, C = 44.28 is the constant such that the probability that the sum of the squares of the sample observations exceeds C is 0.05.
To know more about probability visit :
https://brainly.com/question/29221515
#SPJ11
find the derivative of the function. g ( x ) = ∫ 4 x 2 x u 2 − 5 u 2 5 d u [ hint: ∫ 4 x 2 x f ( u ) d u = ∫ 0 2 x f ( u ) d u ∫ 4 x 0 f ( u ) d u ]
Answers
The derivative of the function g(x) is g'(x) = 28x².
The derivative of the function g(x) can use the Fundamental of Calculus states that if f(x) is continuous on [a, b] then:
∫aˣ f(t) dt is differentiable on (a, b) and its derivative is f(x)
Integral with respect to x by differentiating the integrand with respect to u and then multiplying by the derivative of the upper limit of integration.
We can simplify the given integral using the provided hint:
g(x) = ∫4x²x (u² - 5u²/5)/5 du
g(x) = ∫0²x (u² - 5u²/5)/5 du - ∫0⁴x (u² - 5u²/5)/5 du
The first term on the right-hand side can be integrated as:
∫0²x (u² - 5u²/5)/5 du
= ∫0²x (u²/5 - u²) du
= [tex][(u^3/15) - (u^3/3)]_0^2x[/tex]
= (8x³/15) - (8x³/3)
= -4x³/3
The second term on the right-hand side can be integrated as:
∫0⁴x (u² - 5u²/5)/5 du
= ∫0⁴x (u²/5 - u²) du
=[tex][(u^3/15) - (u^3/3)]_0^4x[/tex]
= (64x³/15) - (64x³/3)
= -32x³
g(x) = -4x³/3 - (-32x³)
= 28x^³/3.
Now, we can differentiate g(x) with respect to x using the power rule:
g'(x) = d/dx [28x³/3]
= 28x²
For similar questions on derivative
https://brainly.com/question/28376218
#SPJ11
A stone is tossed into the air from ground level with an initial velocity of 39 m/s.
Its height at time t is h(t) = 39t − 4.9t^2 m/s. Compute the stone's average velocity over the time intervals
[1, 1.01], [1, 1.001], [1, 1.0001],
and
[0.99, 1], [0.999, 1], [0.9999, 1].
Estimate the instantaneous velocity v at t = 1.
Answers
The instantaneous velocity of the stone at t = 1 is 29.2 m/s.
Given data:
A stone is tossed into the air from ground level with an initial velocity of 39 m/s. Its height at time t is h(t) = 39t − 4.9t² m/s. The required parameters are as follows:
Compute the stone's average velocity over the time intervals [1, 1.01], [1, 1.001], [1, 1.0001],
and [0.99, 1], [0.999, 1], [0.9999, 1].
Estimate the instantaneous velocity v at t = 1.
Solution:
Average velocity = (total distance) / (total time)
In general, distance is the change in the position of an object; as a result, total distance = [h(t2) − h(t1)],
and total time = [t2 − t1].
Using the formula of h(t),
h(t2) = 39t2 − 4.9t²
h(t1) = 39t1 − 4.9t²
Let's evaluate the average velocity over the time intervals using this formula:
[1, 1.01][h(1.01) - h(1)] / [1.01 - 1] = [39(1.01) - 4.9(1.01)² - 39(1) + 4.9(1)²] / [0.01][1, 1.001][h(1.001) - h(1)] / [1.001 - 1]
= [39(1.001) - 4.9(1.001)² - 39(1) + 4.9(1)²] / [0.001][1, 1.0001][h(1.0001) - h(1)] / [1.0001 - 1]
= [39(1.0001) - 4.9(1.0001)² - 39(1) + 4.9(1)²] / [0.0001][0.99, 1][h(1) - h(0.99)] / [1 - 0.99]
= [39(1) - 4.9(1)² - 39(0.99) + 4.9(0.99)²] / [0.01][0.999, 1][h(1) - h(0.999)] / [1 - 0.999]
= [39(1) - 4.9(1)² - 39(0.999) + 4.9(0.999)²] / [0.001][0.9999, 1][h(1) - h(0.9999)] / [1 - 0.9999]
= [39(1) - 4.9(1)² - 39(0.9999) + 4.9(0.9999)²] / [0.0001]
Evaluate the above fractions and obtain the values of average velocity over the given time intervals.
Using the derivative of h(t), we can estimate the instantaneous velocity at t = 1.
Using the formula of v(t), v(t) = h'(t)At t = 1, h'(t) = 39 - 9.8(1) = 29.2 m/s
Thus, the instantaneous velocity of the stone at t = 1 is 29.2 m/s.
To know more about velocity visit:
https://brainly.com/question/18084516
#SPJ11
3)
The domain of this relation does not include which value(s)?
{x,y):y=x2-4}
A)
0
B)
C)
2,0
D)
2,-2
Answers
We can see that the domain of the relation does not include the value of 2 and 0 as when we plug 2 and 0 in the given equation, we get the value of y as zero. Hence, the correct option is (C).
The given relation is{x, y): y = x² - 4}.So, if we plug different values of x to determine the corresponding y-value of the relation, we get:
When x = -2, y = (-2)² - 4 = 0
When x = -1, y = (-1)² - 4 = -3
When x = 0, y = 0² - 4 = -4
When x = 1, y = 1² - 4 = -3
When x = 2, y = 2² - 4 = 0 When x = 3, y = 3² - 4 = 5
From the above values of the relation, we can see that the domain of the relation does not include the value of 2 and 0 as when we plug 2 and 0 in the given equation, we get the value of y as zero. Hence, the correct option is (C).
To know more about domain visit:
https://brainly.com/question/30133157
#SPJ11
If the Gram-Schmidt process �s applied to determine the QR factorization of A. then. after the first two orthonormal vectors q1 and q2 are computed. we have: Finish the process: determine q3 and fill in the third column of Q and R.
Answers
You've completed the Gram-Schmidt process for QR factorization and filled in the third column of matrices Q and R: R(1,3) = a3 · q1, R(2,3) = a3 · q2, R(3,3) = a3 · q3
Given that you already have the first two orthonormal vectors q1 and q2, let's proceed with determining q3 and completing the third column of matrices Q and R.
Step 1: Calculate the projection of the original third column vector, a3, onto q1 and q2.
proj_q1(a3) = (a3 · q1) * q1
proj_q2(a3) = (a3 · q2) * q2
Step 2: Subtract the projections from the original vector a3 to obtain an orthogonal vector, v3.
[tex]v3 = a3 - proj_q1(a3) - proj_q2(a3)[/tex]
Step 3: Normalize the orthogonal vector v3 to obtain the orthonormal vector q3.
q3 = v3 / ||v3||
Now, let's fill in the third column of the Q and R matrices:
Step 4: The third column of Q is q3.
Step 5: Calculate the third column of R by taking the dot product of a3 with each of the orthonormal vectors q1, q2, and q3.
R(1,3) = a3 · q1
R(2,3) = a3 · q2
R(3,3) = a3 · q3
By following these steps, you've completed the Gram-Schmidt process for QR factorization and filled in the third column of matrices Q and R.
Learn more about Gram-schmidt process here:
https://brainly.com/question/30761089
#SPJ11
2. determine whether each of these integers is prime. a) 19 b) 27 c) 93 d) 101 e) 107 f ) 113
Answers
Out of the integers listed, 19, 101, 107, and 113 are prime, while 27 and 93 are not.
To determine if an integer is prime, it must have only two distinct positive divisors: 1 and itself. Here are the results for the integers you provided:
a) 19 is prime (divisors: 1, 19)
b) 27 is not prime (divisors: 1, 3, 9, 27)
c) 93 is not prime (divisors: 1, 3, 31, 93)
d) 101 is prime (divisors: 1, 101)
e) 107 is prime (divisors: 1, 107)
f) 113 is prime (divisors: 1, 113)
Learn more about integers here:
https://brainly.com/question/1768254
#SPJ11
The test scores for the students in two classes are summarized in these box plots.
• The 20 students in class 1 each earned a different score.
• The 12 students in class 2 earned a different score.
What is the difference between the number of students who earned a score of 90 or greater in class 2 and the number of students who earned a 90 or greater in class 1?
A. 1
B. 2
C. 5
D. 7
Answers
The difference between the number of students who earned a score of 90 or greater in class 2 and those who earned a 90 or greater in class 1 is 1.
The test scores for the students in the two classes are summarized in these box plots. To find the difference between the number of students who earned a score of 90 or greater in class 2 and the number of students who earned a 90 or greater in class 1, we need to count the number of students that earned 90 or greater in each class and take the difference.
The answer to this question is the difference between the number of students who earned a score of 90 or greater in class 2 and those who earned a 90 or greater in class 1. We can get this by counting the number of students who score 90 or greater in each class and then taking the difference between the two. The box plot for class 1 shows that there is only one student who has a score of 90 or greater.
The box plot for class 2 shows that two students scored 90 or greater. Thus, the difference between the number of students who earned a score of 90 or greater in class 2 and those who earned a 90 or greater in class 1 is 2 - 1 = 1. Therefore, the correct option is A: 1.
To find the difference between the number of students who earned a score of 90 or greater in class 2 and the number of students who earned a 90 or greater in class 1, we need to count the number of students that earned 90 or greater in each class and take the difference. A box plot is a graphical dataset representing the median, quartiles, and extreme values. It is used to depict data distribution visually. In the question, two box plots represent the data of two different classes.
The box plot for class 1 shows that there is only one student who has a score of 90 or greater. The box plot for class 2 shows that two students scored 90 or greater. We can see that the box plot of class 1 is short and has only one whisker pointing up, indicating that there is only one student who scored higher than the median. The box plot of class 2, on the other hand, is longer and has two whiskers pointing up, indicating that two students scored higher than the median.
Therefore, the difference between the number of students who earned a score of 90 or greater in class 2 and those who earned a 90 or greater in class 1 is 1.
To know more about the median, visit:
brainly.com/question/300591
#SPJ11
(7 points) assuming you have a valid max-heap with 7 elements such that a post-order traversaloutputs the sequence 1, 2, . . . , 6, 7. what is the sum of all nodes of height h = 1?
Answers
The sum of all nodes of height h = 1 is 6.
In a max-heap, the parent node always has a higher value than its children. Additionally, in a post-order traversal of a max-heap, the parent node is visited after its children.
Given that the post-order traversal outputs the sequence 1, 2, ..., 6, 7, we can determine the heights of the nodes as follows:
Node 7: Height 0 (root)
Node 6: Height 1
Nodes 1, 2: Height 2
Nodes 3, 4, 5: Height 3
To find the sum of all nodes of height h = 1, we need to consider the nodes at height 1, which in this case is just Node 6.
Know more about node here:
https://brainly.com/question/30885569
#SPJ11
in the one-way anova, the within-groups variance estimate is like _________ in two-way anova.
Answers
In one-way ANOVA, the within-groups variance estimate is like the error term in two-way ANOVA.
In one-way ANOVA, the within-groups variance estimate (also known as the error variance) measures the variability of the observations within each group. It is an estimate of the variation in the response variable that is not accounted for by the differences between the group means. The within-groups variance estimate is used to calculate the F-statistic, which is used to test whether there are significant differences among the means of the groups.
In two-way ANOVA, there are two factors that can affect the response variable. The within-groups variance estimate in two-way ANOVA is also an estimate of the variability of the observations within each group, but it takes into account the effects of both factors on the response variable. The within-groups variance estimate in two-way ANOVA is used to test for the main effects of the two factors, as well as their interaction effect. The error term in two-way ANOVA is used to calculate the F-statistic for each effect, and the p-value associated with each F-statistic is used to determine whether the effect is statistically significant.
To learn more about variance visit:
brainly.com/question/14116780
#SPJ11